4. Stability Statistics
These figures aim to evaluate the robustness and stability of a trading system or strategy by calculating statistics based on less complex figures. Stability is the key to improve performance through money management strategies. A proper use of leverage can only be done if the trading edges are well measured.
Win Rate
The percentage of profitable trades, the Win Rate, is another statistic that many traders use to gauge performance success. This figure, sometimes referred to as Success Rate or Profitability, has to do with the reliability of the trading method. It’s simply the number of winning trades expressed as a percentage of the total number of trades. It is calculated as following:
Win Rate = Number of Profit Trades X 100 / Total Number of Trades
On a random entry method with no edge - for instance, a “coin toss” approach, - the Win Rate will directly be in line with the Risk-to-Reward Ratio. A system entering a trade based on coin toss heads for short and tails for long, each day at 10:30am, with a Stop Loss of 50 pips and a Take Profit of 20 pips, will hit the Take Profit more times than the Stop Loss. This doesn't mean the system would make money, because even with a 70% Win Rate it would result in a break-even or losing system because of the impact of spreads and slippage. But in any case, a 5:2 Risk-to-Reward Ratio provides a positive baseline probability.
Loss Rate
This is the percentage of unprofitable trades in a trading report. It is important to know that this number does not derive automatically from the above by subtracting that one from 100%. In trading, there are not only winning and losing trades but also break-even trades.
Loss Rate = Number of Loss Trades X 100 / Total Number of Trades
Break-even Rate
This is not a very common statistical measure but nonetheless very useful. This is the percentage of break-even trades in a trading report, the proportion of trades that were neither winning nor losing trades.
Break-even Rate = Number of Break-even Trades X 100 / Total Number of Trades
If we were to compare two systems with an equal Win Rate of 55%, this figure would be of utmost importance if one of the system would have a Break-even rate of 0% and the other one of 15%. We can deduce from a 15% Break-even Rate and a 55% Win rate that the Loss Rate is only 20%, while for a system with no break-even trades, the Loss Rate is 45%. A 55% Win Rate for a 20% Loss Rate is still a very good ratio, even if the system has such a modest Win Rate.
Risk-to-Reward Ratio
The Risk-to-Reward Ratio is the maximum risk taken on a particular trade divided by the maximum profit expectation of the same trade. It’s a value used to estimate particular trade set-ups and should be not used as the Payoff Ratio.
Risk Reward Ratio = maximum risk taken on a particular trade / maximum profit expectation of the same trade
The Risk-to-Reward is a dynamic property considering the Favorable and Adverse Excursions of a trade (see Trade Statistics). Let's suppose you open a trade with a 500 pip target and a 100 pip stop. At the point it reaches 480 pips, your risk is still the same if you don't protect part of the profits. If you do, the Risk-to-Reward will change accordinlgy. Moving a stop to the entry price, for example, is removing the risk from the trade.
Sunil Mangwani offers an instructive webinar titled: “Understanding the simple rules of Money Management – Part I: The Risk-to-Reward ratio”- It goes into the topic of the next LC chapter, nevertheless it will help you to understand why this ratio is important to control risk when analyzed in a broader statistical report.
Win/Loss Ratio
This figure is purely the total number of winning trades compared to the total number of losing trades. If in 100 trade,s you have 50 winners and 50 losers, then your win/loss ratio is 50:50. Alternatively, if you have 70 winners and 30 losers then the ratio is 7:3, etc.
Opposed to the Risk-to-Reward Ratio it does not take into account how much was won or lost, but simply if they were winners or losers. The formula is:
Win/Loss Ratio = Number of Winning Trades / Number of Losing Trades
It is important to remember that this ratio is not the only a factor in determining if and how profitable a system is. It is also important to calculate how much it wins when it is right vs. how much it loses when it is wrong.
Standard Deviation
One of the most meaningful ways to evaluate the profitability is through the standard deviation figure. Standard deviation measures how widely the trades results are dispersed from the average results. The dispersion is defined as the difference between the actual value and the average value.
The larger the difference between the actual trade result and the average result, the higher the standard deviation and volatility of the Equity Curve will be. The closer the results are to the average, the lower the standard deviation or volatility of the Equity Curve.
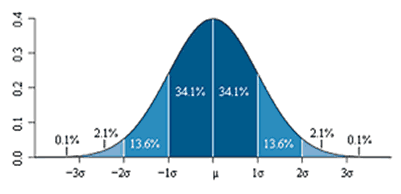
In order to calculate the Standard Deviation, take the square root of the variance, the average of the squared deviations from the mean value. One standard deviation away from the mean (the Average Profit per trade), either plus or minus, will include 67.5% of the trade results. Two standard deviations on either side of the Average Profit figure will encompass approximately 95% of all probable outcomes when trading a certain system.
ST High Range = 2 x Standard Deviation + Average Profit
ST Low Range = Average Profit - 2 x Standard Deviation
This means that 95% of the time, this system would have returned profits in the range outlined above.
If the returns are widely dispersed with both large winners and losers, the performance shows a high Standard Deviation and is therefore considered risky. Conversely, if returns are wrapped tightly around the mean, the performance has a smaller Standard Deviation and is considered less risky.
The below picture shows a normal distribution of where the frequency of the occurrence of results is distributed like a bell curve around the mean value. This means that the density of the results is highest near the center of the range of results.
Average Profitability
Average Profitability per trade basically refers to the average amount you can expect to win or lose per trade, but its calculation differs from the previous Payoff Ratio. Accordingly to Grace Cheng, this is the formula:
Average Profitability Per Trade = (Win Rate x Average Profit) - (Loss Rate x Average Loss)
Let's imagine a hypothetical scenario of a performance record showing a 30% Win Rate and a Payoff Ratio of 2:1. In this case, the resulting value would be a negative one, meaning the supposed benefit of having a 2:1 payoff ratio does not compensate a 70% Loss Rate.
In a scenario of a Payoff of 1:3 you would need a Win Rate 80% to get some decent positive Average Profitability and be profitable over time.
The number should be expressed in dollar values rather than in pips because of the oscillations of the pip value. But what is most important here is the number to be positive.
Profit-to-Drawdown Ratio
This ratio measures the amount of profit you experience for a given amount of Drawdown.
For example, a performance that shows a 20% profit after a 20% Drawdown should be considered better than a performance that reaches a 20% profit after a 60% Drawdown.
In order to calculate the Profit to Drawdown Ratio, the Net Profit has to be divided by the Maximum Drawdown for a certain period of time. Accordingly to Lars Kestner,
The higher the number, the better as it means there is more profit generated for a given amount of Drawdown. In this sense, it creates a measure of Risk-to-Reward. Riskier strategies have larger Maximum Dradowns and will lead to lower Profit-to-Drawdown Ratios.”
Profit to Drawdown Ratio = Total Net Profit / the Maximum Drawdown
Source: “Quantitative Trading Strategies” by Lars Kestner, McGraw-Hill, 2003, pag.82
Another way to calculate this figure shows how much money the system gave back after making a new equity high. This measurement helps the trader determine if a certain method is appropriate for his/her trading temperament.
It's calculated by subtracting two Standard Deviations from the Average Profit figure and then adding two Standard Deviations to the Average Drawdown figure. These numbers are taken from a Monte Carlo simulation. The result show a hypothetical ratio based on how much profit giveback the trading performance manifests.
Donald W. Pendergast Jr. says that typically a system with a Profit-to-Drawdown ratio of 8 to 1 or better is considered very tradable. He goes on to explaining that:
While at first glance it appears as if we've discovered a reasonable tradable system [...], we now need to consider the possibility that the real-world results could be closer to the minimum profit figure.”
Source: “Trade System Evaluation” by Donald W. Pendergast Jr., Technical Analysis of Stocks & Commodities Magazine, March 2009, pag. 14
Note this figure is also part of the Monte Carlo simulation. This results in a much smaller ratio, by taking minimum profit figure and dividing it by the Maximum Absolute Dollar Drawdown.
What is a Monte Carlo simulation? Some statistical figures depend on the order of trades. One of these is the Number of Consecutive Losses and another one is the Drawdown figure in its several variations. Other figures will also depend on the order of the trades, except if all trades have the same position size. One way to account for trade ordering effects is the Monte Carlo simulation.
This computational technique, used in simulation of trading models, creates a randomly sampled statistical distribution of trade sequences. When using Monte Carlo analysis to simulate trading, the trade distribution, as represented by the list of trades, is sampled to generate a trade sequence. Each sequence is analyzed, and the results are sorted to determine the probability of each result.
Sharpe Ratio
Developed by Nobel Laureate William Sharpe, the Sharpe Ratio is a standard in the money management industry and is used to evaluate the Risk-to-Reward efficiency of investments. The Sharpe Ratio is calculated by subtracting the risk-free rate - such as the one of the US Treasury bond - from the Return Rate and dividing the result by the Standard Deviation of the system's returns. The Sharpe ratio formula is:
Sharpe Ratio = (Return Rate – Risk free rate) / Standard Deviation
Following John L. Person explained in a detailed fashion:
You will divide the average of the excess returns (the returns generated by the strategy minus the risk-free return) by the standard deviation of the returns and then calculate the average monthly return over some number of months, say, 12 months, by averaging the returns for the 12 months. You also calculate the standard deviation of the monthly returns over the same period. Then you annualize the numbers by multiplying the average monthly return by 12 and then multiplying the standard deviation of the monthly returns by the square root of 12.(...)
To further calculate, you need an input value for the risk-free return (Treasury bill rate), which is the annualized return. You now calculate what we consider the excess return, which is the annualized return achieved by your investment in excess of the risk-free rate of return available. This is the extra return you receive by assuming some risk.”
Source: "Forex Conquered: High Probability Systems and Strategies for Active Traders" by John L. Person, Wiley, 2007, pag.-202-203
The Sharpe Ratio is thus the average percent change in equity of each period over the Standard Deviation of those values. Higher Sharpe Ratios indicate that a greater amount of average profit could be made with less day-to-day volatility.
Calmar Ratio
Another performance number that new traders rarely look at is the Calmar Ratio. Although there are numerous variations and twists to it, in its simplest form this number is the ratio of Annual Return Rate to the Maximum Drawdown, using the absolute value. It is similar to the Sharpe Ratio, with the difference that it's based on the worst case scenario, rather than on volatility.
If a performance record shows a 50% annual Return Rate with 25% Maximum Drawdown, the Calmar ratio will be 2.
Calmar Ratio = Compounded Annual Return / Maximum Drawdown
By including the Calmar Ratio in your evaluation arsenal, you will be much better prepared to properly scrutinize your trading methods and compare them more efficiently.
R-multiple
R-multiples is the initial risk taken on each trade. It's not a statistical figure in itself but it serves for the calculation of Expectancy.
For example, if you buy the EUR/USD at 1.5000 and set the Stop Loss at 1.4900. This means if the trade results in a loss, it would be a loss of of 100 pips. In short, you R is 100 pips. But you are able to sell the pair back at 1.5300 and make 300 pips in profit. This means the final outcome in this trade is +3R.
The formula is thus:
R-multiple = ( Profit amount / Initial R )
When you have a series of profits and losses expressed as Risk-to-Reward ratios, what you really have is what Van Tharp calls an R-multiple distribution. This means that any trading system can be characterized as being an R-multiple distribution. When you have an R-multiple distribution from your trading system, you need to get the average of that distribution – that is the system’s expectancy.
Average R-Multiple
This statistic is another way to assess how much one expects to gain for every dollar bet or risked on a given trade. Numbers greater than zero point to a winning system, less than zero to a losing system. The formula to calculate it is:
Average R-Multiple = ( Total Win Percent – Total Loss Percent ) / Total Risk Percent
Expectancy
Van Tharp describes Expectancy only in reference to R-multiples of a hard Stop Loss, so the maximum risk can be calculated for every trade.
This figure gives you the average R-value that you can expect from the system over many trades. In other words, Expectancy tells you how much you can expect to make on the average, per dollar risked, over a number of trades.
You can calculate the mathematical expectation of a system by the following formula:
Expectancy = (Average Profit X Win Rate) - (Average Loss X Loss Rate)
This formula requires that you take into account both the Win Rate and the Payoff Ratio when estimating the long-term profit potential. For example, a system with 50% accuracy and the 2 to 1 Payoff Ratio has an expectancy equal to 0,5. This means you can expect to earn 50% of the amount that you risk per trade on average. If you risk 2% of your capital per trade you can expect to earn 1% per trade (50% of 2%) on average with such a system. The formula looks like this:
Expectancy = (1+ Average Profit / Average Loss) X (Win Rate) -1
Short-term traders normally achieve higher Win Rate, while long-term traders generally achieve greater Profit factors (Average Profit / Average Loss). But both strive to have a positive Expectancy.
Negative mathematical expectation means you will lose your money over the long-term no matter how small or big your positions are. This happens for instance in a Casino where the mathematical expectation is always negative. And a zero expectation means you can expect your account to fluctuate around breakeven for ever. Ralph Vince states about this figure:
The difference between a negative expectation and a positive one is the difference between life and death. It doesn't matter so much how positive or how negative your expectation is; what matters is whether it is positive or negative.
Source: “The Mathematics of Money Management: Risk Analysis Techniques for Traders". By Ralph Vince, John Wiley and Sons, 1992, p. 18





